Exploring repeated measures data: Random coefficient regression models in action

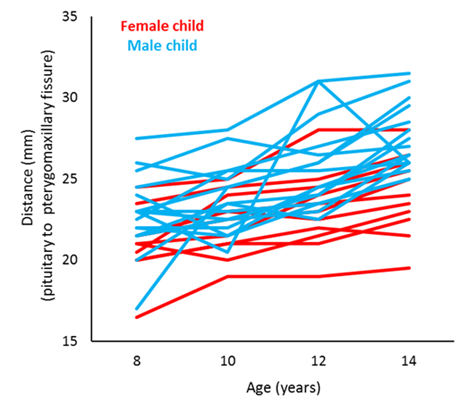
A random coefficient regression is a special type of linear mixed model. They can be used when we want to explore the relationship between a response variable (y) and a continuous explanatory variable (x) and we have repeated measurements of x and y on individual subjects. Whereas in ordinary regression there is a single fixed value for each parameter (e.g., the intercept and slope), random coefficient regression allows these parameters to be unique for each subject. This is done by modelling all the coefficients of the regression model for each subject simultaneously using random effects and, importantly, allowing for correlation among these random effects.

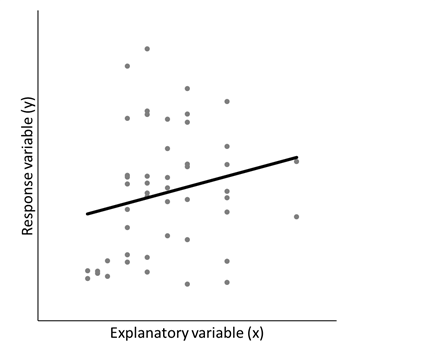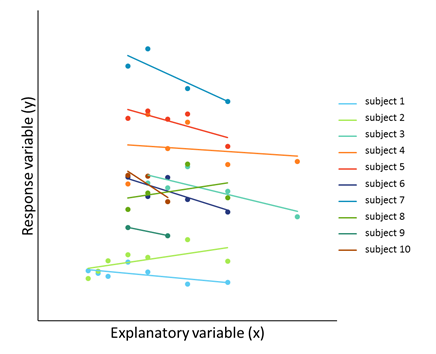The conceptual difference between ordinary regression (left) and random coefficient regression (right)

Analyzing orthodontic growth profiles: A case study

To illustrate, let’s consider some repeated measures data on the orthodontic growth rate of children (Potthoff and Roy, 1964). [1] In this study, researchers at the University of North Carolina Dental School tracked the orthodontic growth of 27 children by measuring the distance between the pituitary and the pterygomaxillary fissure every 2 years from the ages of 8 to 14 years.

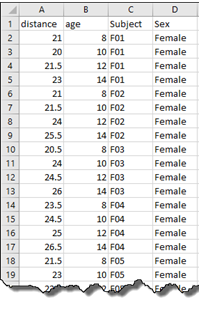
The data set contains two variates: 

• distance, the response variable
• age, age of the child in years

And two factors:

• Subject, identifying the individual children on whom repeated measures were taken
• Sex, the sex of the child

Comparing growth profiles: Females vs. males

Of interest is comparing the orthodontic growth profiles between female and male children. We can do this by using random coefficient regression. Here, we aim to model the orthodontic growth profiles of female and male children over age, allowing for random variation about the regression parameters for the individual children.

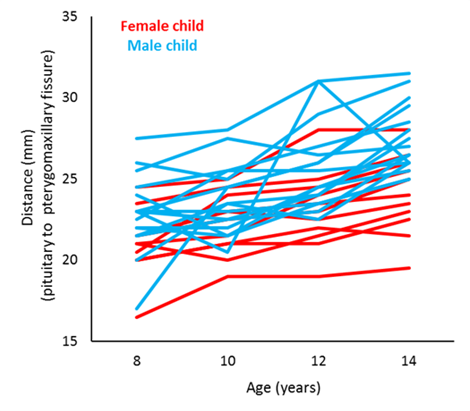Graph of the orthodontic growth profiles of the individual children coloured by sex.

The mechanics of model fitting

To do this we fit a fixed effect for Sex and allow the fixed age covariate effect to differ between the two sexes. That is: Sex + age + Sex.age, where Sex.age represents an interaction term.

We also need to fit correlated random intercept and slope deviations for the individual children. That is, we specify our random model such it generates

• a set of child intercepts with a common variance ()
• a set of child slopes with a common, but different, variance ()

such that

• the intercepts and/or slope from any two different children are independent

BUT

• the intercept and slope deviations from any given child are correlated ().

Variance-covariance matrix = I ⊗ C where C =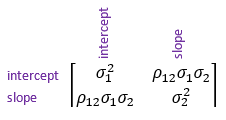

Mastering random coefficient regression with Genstat or ASReml-R

Our tutorial videos will teach you more about how to analyse your data using a random coefficient regression in Genstat or ASReml-R.

Random Coefficient Regression in Genstat

Random coefficient regression in ASReml-R 4

Defining complex variance structures in MMA: Part 2-Random Coefficient Regression

Citation

 [1] Potthoff, R. F. and Roy, S. N. (1964), A generalized multivariate analysis of variance model useful especially for growth curve problems, Biometrika, 51, 313–326.