Statistical outliers: Should you toss them or treasure them in your analyses?
The VSNi Team
17 May 2021
Outliers are sample observations that are either much larger or much smaller than the other observations in a dataset. Outliers can skew your dataset, so how should you deal with them?
Outlier adventures: a case study in sales analysis
Imagine Jane, the general manager of a chain of computer stores, has asked a statistician, Vanessa, to assist her with the analysis of data on the daily sales at the stores she manages. Vanessa takes a look at the data, and produces a boxplot for each of the stores as shown below.
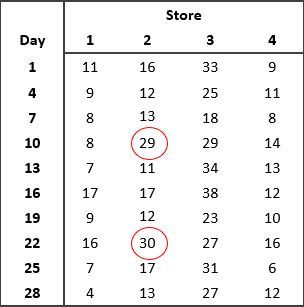
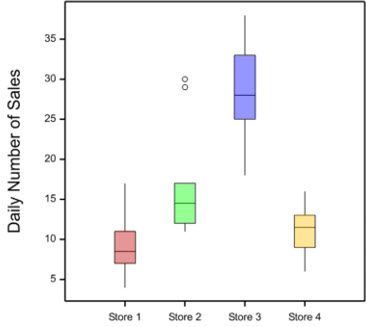
What do you notice about the data?
Vanessa pointed out to Jane the presence of outliers in the data from Store 2 on days 10 and 22. Vanessa recommended that Jane checks the accuracy of the data. Are the outliers due to recording or measurement error? If the outliers can’t be attributed to errors in the data, Jane should investigate what might have caused the increased sales on these two particular days. Always investigate outliers - this will help you better understand the data, how it was generated and how to analyse it.
To drop or not to drop?
Vanessa explained to Jane that we should never drop a data value just because it is an outlier. The nature of the outlier should be investigated before deciding what to do.
Whenever there are outliers in the data, we should look for possible causes of error in the data. If you find an error but cannot recover the correct data value, then you should replace the incorrect data value with a missing value.

However, outliers can also be real observations, and sometimes these are the most interesting ones! If your outlier can’t be attributed to an error, you shouldn’t remove it from the dataset. Removing data values unnecessarily, just because they are outliers, introduces bias and may lead you to draw the wrong conclusions from your study.
Transforming data and exploring alternative models
- Transform the data: if the dataset is not normally distributed, we can try transforming the data to normalize it. For example, if the data set has some high-value outliers (i.e. is right skewed), the log transformation will “pull” the high values in. This often works well for count data.
- Try a different model/analysis: different analyses may make different distributional assumptions, and you should pick one that is appropriate for your data. For example, count data are generally assumed to follow a Poisson distribution. Alternatively, the outliers may be able to be modelled using an appropriate explanatory variable. For example, computer sales may increase as we approach the start of a new school year.
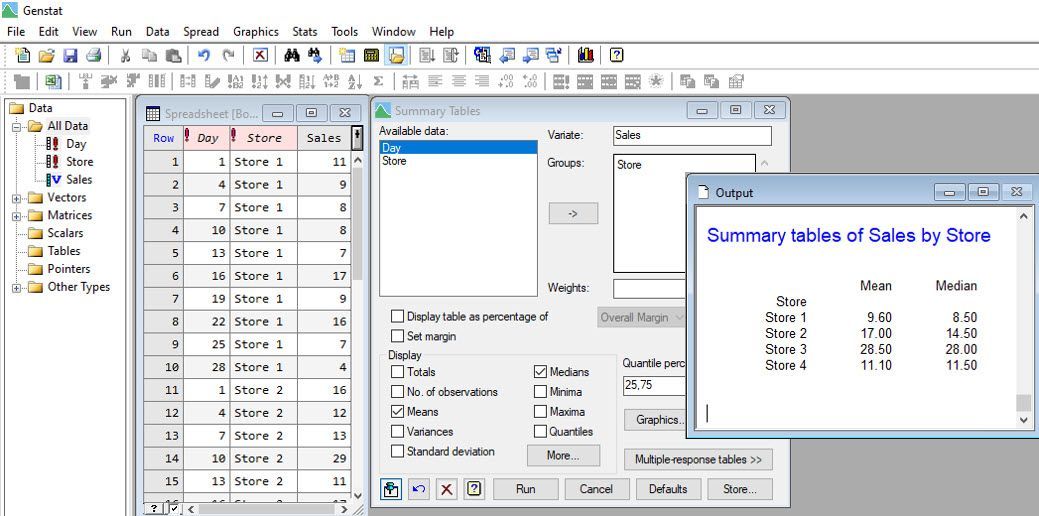
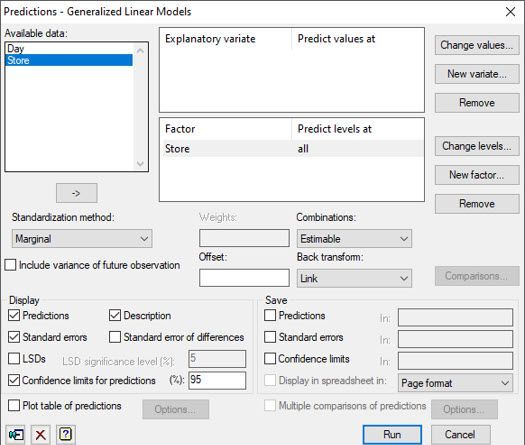
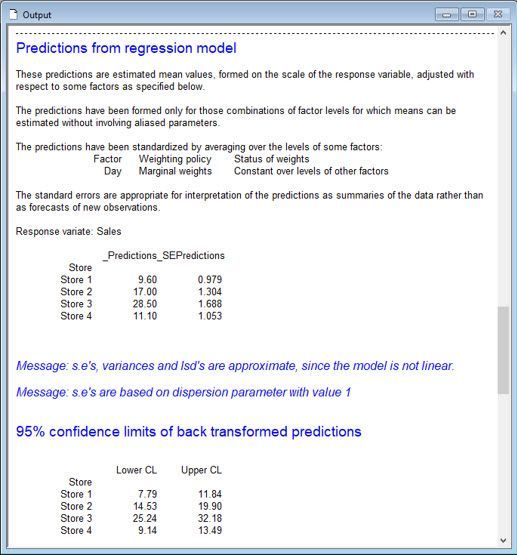
In our example, Vanessa suggested that since the mean for Store 2 is highly influenced by the outliers, the median, another measure of central tendency, seems more appropriate for summarizing the daily sales at each store. Using the statistical software Genstat, Vanessa can easily calculate both the mean and median number of sales per store for Jane.
Vanessa also analyses the data assuming the daily sales have Poisson distributions, by fitting a log-linear model.
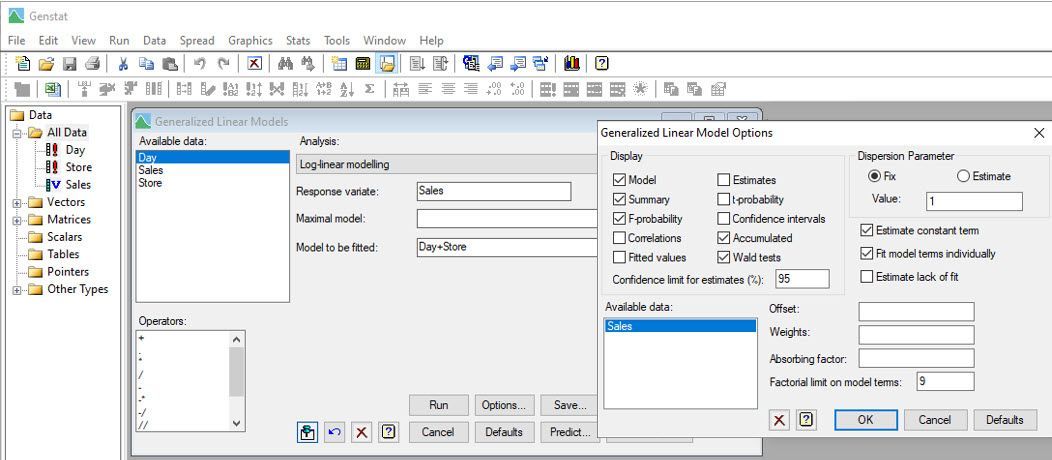
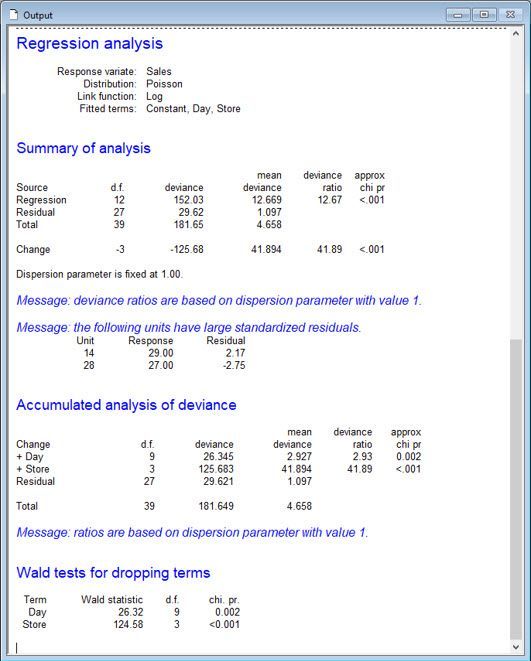
Notice that Vanessa has included “Day” as a blocking factor in the model to allow for variability due to temporal effects.
From this analysis, Vanessa and Jane conclude that the means (of the Poisson distributions) differ between the stores (p-value < 0.001). Store 3, on average, has the most computer sales per day, whereas Stores 1 and 4, on average, have the least.
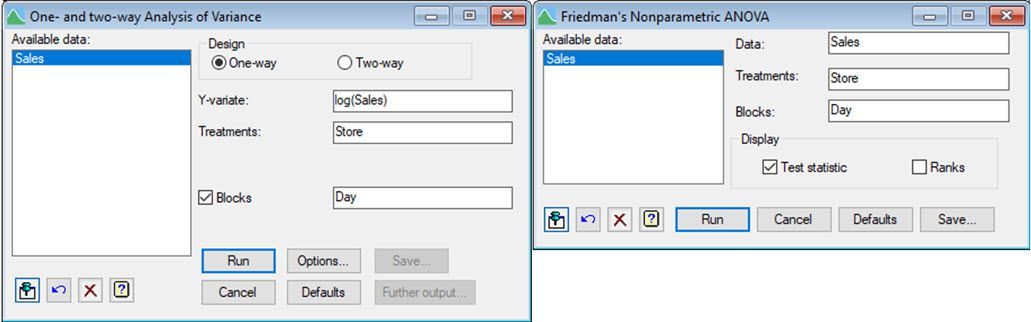
There are other statistical approaches Vanessa might have used to analyse Jane’s sales data, including a one-way ANOVA blocked by Day on the log-transformed sales data and Friedman’s non-parametric ANOVA. Both approaches are available in Genstat’s comprehensive menu system.
Best practices for dealing with outliers
There are many ways to deal with outliers, but no single method will work in every situation. As we have learnt, we can remove an observation if we have evidence it is an error. But, if that is not the case, we can always use alternative summary statistics, or even different statistical approaches, that accommodate them.
Popular
Related Reads
