Improving the design of your experiments part 1: a-priori blocking

Design of experiments is a mature field with many useful designs and good practical recommendations. You’ve probably heard about the need for reasonable replication, good control (or blocking) and proper randomization of your treatments. These are topics most of us have studied before, and we must consider them when designing our experiments.

Unique considerations for breeding trials

Breeding trials for agronomy or forestry have some particular characteristics that set them apart from the other experiments. To begin with, we usually have many genotypes, typically in the hundreds, that we want to evaluate simultaneously. In addition, we often have only a limited number of replications for each of our treatments (genotypes, lines, families, etc.).

The above implies that we often have to evaluate our genotypes in large trials that inherently will not be as spatially homogenous as we will like. For that reason, using a completely randomized design (CRD) is a very poor decision. Hence, we typically establish a randomized complete block design (RCBD) as a better alternative that incorporates some blocking to help us control for sources of variability. But RCBDs, still have their issues. For example, if we evaluate 288 genotypes and each is replicated four times, then we would form 4 blocks (or replicates) and our study would have a total of 1,152 plots. In this case, each replicate (or block) will contain 288 experimental units in order to ensure that each of them has a single copy of each genotype. However, having this large replicate area as a homogeneous blocking unit is likely unrealistic. In order to deal with this, we move to more complex experimental designs that better control the spatial variability within a replicate.

Incomplete block designs

Here is where the incorporation of some good a-priori blocking at the stage of planning is always a good practice! The most widespread option is to use an incomplete block design (IBD). This design splits our original full replicate (say of size 288) into smaller subunits, where each contains a portion of the genotypes. For example, we can subdivide the full replicate into 8 subunits each with a total of 36 plots (or genotypes). These correspond to the incomplete blocks, and they can be defined with convenient shapes, for example 6x6 (6 rows by 6 columns, see figure below). But we have many other options (such as 2x18, 3x12 and 4x9, to name a few).

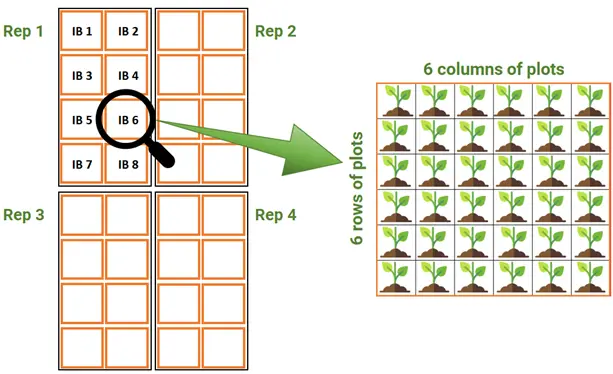
Depending on how these designs are generated (and considering some restrictions on design parameters); these include alpha designs, cyclic designs, Youden square designs, balanced and partially-balanced incomplete block designs, lattice designs, etc. We do not specify their differences here, but you’ve probably heard these names before.

Note - one crucial element of these designs is the size of the incomplete block; importantly:

• They should be small enough to be able to describe in the field a homogenous blocking unit. 
• They should be large enough to allow several (but not necessarily all) pairs of treatments to be compared within the same blocking unit.

If the blocks are too large they will still be too variable to help control for field heterogeneity. If they are too small you will be highly limited to contrast many of the treatment pairs. In addition, we need to add that if you make your blocks too small (say with only 4 genotypes), once you fit the block effect, you run the risk of confounding the genetics with the blocks, and therefore your incomplete block effect might ‘absorb’ your genetic signal!

As you can imagine, there is a balance between the number of treatments, the size of your incomplete block, and the number of replicates per genotype. This is what makes deciding upon the final design challenging. But there are plenty of recommendations around and you can always use specialized software to generate these experiments. For example, CycDesigN generates a wide variety of design types, allowing you to create an optimal or near optimal design for your trial.

Row-column designs

There is another good alternative that uses small subunits to control for field variability. This is the row-column design (RCD). These designs allow for blocking in two-directions: along both rows and columns. For breeding trials, the row and column subunits represent a form of incomplete blocks, but now they run perpendicular to each other. For our example, with 288 plots in a full replicate laid out across 24 rows by 12 columns (see figure below), then we can have 24 incomplete blocks running in one direction and 12 in another.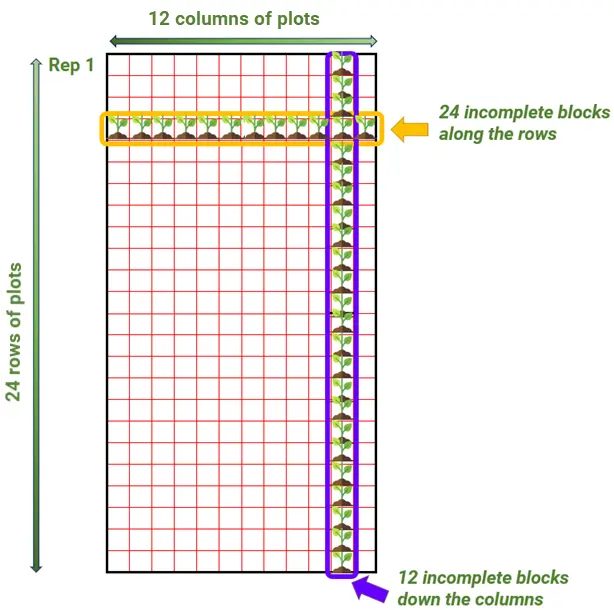

RCDs are a good option when we have to control for variability in two dimensions. Setting the dimensions of the rows and columns requires similar logic as for IBDs; that is, using subunits that are not too large and not too small. 

One interesting characteristic of RCDs is that they are very similar to some designs we learnt about in our statistics training: Latin squares. But one advantage of RCDs is that their two dimensions do not need to be the same and identical to the number of treatments. This implies that they are very flexible, allowing for a wide array of options. Once more, we can use sophisticated software (such as CycDesigN) to generate randomized RCDs.

IBDs versus RCDs

But, when to use which design? In our available testing area (field, laboratory or greenhouse), often we can easily fit any of these two designs. However, it may not be clear which one is more suitable. The answer lies in the nature of the spatial variability we are expecting to find. 

IBDs are better in patchy environments. For example, if we expect to have several small areas (e.g., lumps) with similar nutrient and water availability conditions. There might be several of these patches, and they will probably vary in size, but we expect to be able to describe them (at least partially) with an incomplete block. Hence, the size and shape of the incomplete blocks should consider the characteristics of these patches.

In contrast, RCDs will model heterogeneity dominated by trends, and ideally those trends should be aligned with the directions of the rows and/or columns of the full replicate. In this case, these blocking units identify long subunits that describe similar conditions in these trends. For example, think about a greenhouse with a temperature trend from front to back. It is common to also identify these subunits as rows within replicate or columns within replicate, and not across replicates. This will allow us to make them small enough to describe the field patterns properly.

It is also important to consider that most field trials are arranged in a two-dimensional space, and for this reason, we anticipate that there might be some important variation in one or both directions. Here, the use of an RCD represents insurance for these possible sources of variability.

Random or fixed blocks

In both of the above designs, given the nature of having incomplete blocking units, these should be considered in the linear model as random effects, in order to recover inter-block information. Therefore, there will be a variance component associated with the blocks in an IBD, and with rows and columns in an RCD. 

This analytical approach, with the random incomplete blocks, will indirectly allow for some form of spatial control, as records from plots within the same level of a subunit will be modelled as correlated observations. This should improve the overall analyses. 

Final words: the complexity and benefits of a-priori blocking

Note that there are many other possible designs and variants that can allow for some form of blocking structure (see for example, Latinization), and other options that allow for good neighbour balance (NB) and evenness of distribution (ED) properties, but we direct you to the specialized literature for further details. You will find that these a-priori blocking techniques make the generation of the design more complex, their establishment in the field more laborious, and their statistical analyses more demanding! But modern and sophisticated blocking structure constitutes a form of ‘insurance’ to control for potential future, expected or un-expected, field variability in the form of patches and/or trends. And given that the technology (and software) is available, we strongly recommend the use of a-priori blocking on a routine basis. Also, it is easier and cheaper to focus our efforts on using a good design before establishing our experiment than on trying to recover information at the analysis stage from a poorly designed experiment!

Recommended literature for further exploration

Kuehl, R.O. 2000. Design of Experiments: Statistical Principles of Research Design and Analysis. 2nd Edition. Brookes/Cole. Pacific Grove, California.

Piepho, H-P., Williams, E.R., and Volker, M. 2020. Generating row-column field experimental designs with good neighbour balance and even distribution of treatment replications. J Agron Crop Sci 207(4): 745-753.

Williams. E.R., Matheson, A.C. and Harwood, C.E. 2002. Experimental Design and Analysis for Tree Improvement. 2nd Edition. CSIRO Publishing.

About the author

Dr. Salvador Gezan is a statistician/quantitative geneticist with more than 20 years’ experience in breeding, statistical analysis and genetic improvement consulting. He currently works as a Statistical Consultant at VSN International, UK. Dr. Gezan started his career at Rothamsted Research as a biometrician, where he worked with Genstat and ASReml statistical software. Over the last 15 years he has taught ASReml workshops for companies and university researchers around the world. 

Dr. Gezan has worked on agronomy, aquaculture, forestry, entomology, medical, biological modelling, and with many commercial breeding programs, applying traditional and molecular statistical tools. His research has led to more than 100 peer reviewed publications, and he is one of the co-authors of the textbook Statistical Methods in Biology: Design and Analysis of Experiments and Regression.