Decoding hypothesis testing: investigating type I and type II errors

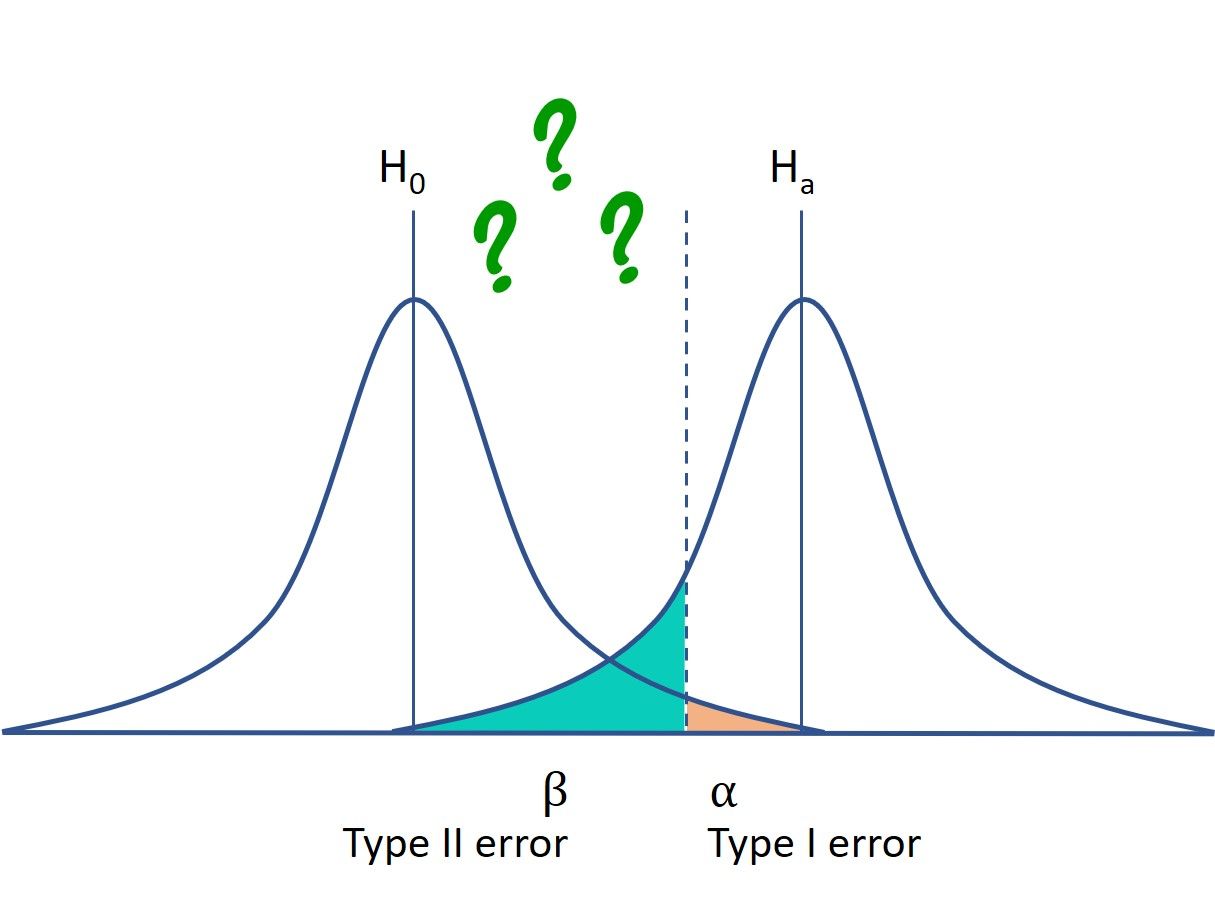
Hypothesis testing is the art of making decisions using data. It involves evaluating two mutually exclusive statements: the null hypothesis and the alternative hypothesis . The strength of evidence against the null hypothesis, as provided by the observed data, is often measured using a p-value. The smaller the p-value, the stronger the evidence against the null hypothesis. You can learn more about p-values in one of our previous blogs.

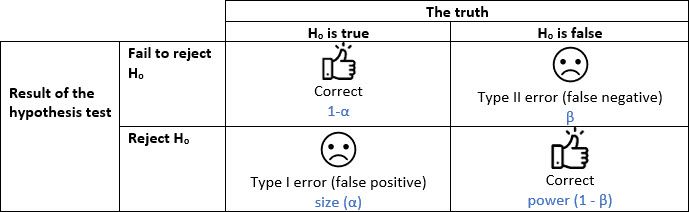
When we make a decision using a hypothesis test there are four possible outcomes: two representing correct decisions and two representing incorrect decisions. The incorrect decisions are due to either Type I or Type II errors.

The illusory verdict: unraveling type I errors

A Type I error, or a false positive, occurs when we reject the null hypothesis when in fact it is true. In other words, this is the error of accepting the alternative hypothesis when the results can be attributed to chance. In hypothesis testing, the probability of making a Type I error is often referred to as the size of the test or the level of significance and denoted by alpha (α). Typically, the Type I error rate is set to 0.05 giving a 1 in 20 chance (i.e. 5%) that a true null hypothesis will be rejected.  

Missed opportunities: the enigma of type II errors

A Type II error is a false negative. This occurs when we fail to reject the null hypothesis when in fact it is false. The probability of making a Type II error is usually denoted by β and depends on the power of the hypothesis test (β = 1 - power). You can reduce the chance of making a Type II error by increasing the power of your hypothesis test. Power can be increased by increasing the sample size, reducing variability (e.g. by blocking) or decreasing the size of the test.

About the author

Dr Vanessa Cave is an applied statistician interested in the application of statistics to the biosciences, in particular agriculture and ecology, and is a developer of the Genstat statistical software package. She has over 15 years of experience collaborating with scientists, using statistics to solve real-world problems.  Vanessa provides expertise on experiment and survey design, data collection and management, statistical analysis, and the interpretation of statistical findings. Her interests include statistical consultancy, mixed models, multivariate methods, statistical ecology, statistical graphics and data visualisation, and the statistical challenges related to digital agriculture.

Vanessa is currently President of the Australasian Region of the International Biometric Society, past-President of the New Zealand Statistical Association, an Associate Editor for the Agronomy Journal, on the Editorial Board of The New Zealand Veterinary Journal and an honorary academic at the University of Auckland. She has a PhD in statistics from the University of St Andrew.